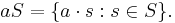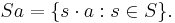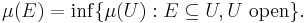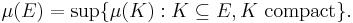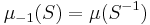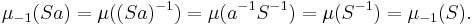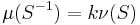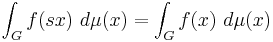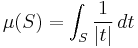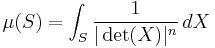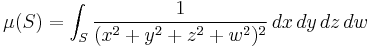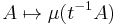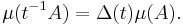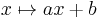Haar measure

In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups.

This measure was introduced by Alfréd Haar, a Hungarian mathematician, in 1933.^[1] Haar measures are used in many parts of analysis and number theory, and also in estimation theory.

1 Preliminaries
2 Haar's theorem
3 The right Haar measure
4 Haar integral
5 Examples
6 Uses
7 The modular function
8 See also
9 Notes
10 Further reading
11 External links

Preliminaries

Let G be a locally compact topological group. In this article, the σ-algebra generated by all compact subsets of G is called the Borel algebra.^[2] An element of the Borel algebra is called a Borel set. If a is an element of G and S is a subset of G, then we define the left and right translates of S as follows:

Left translate:

$a S = \{a \cdot s: s \in S\}.$

Right translate:

$S a = \{s \cdot a: s \in S\}.$

Left and right translates map Borel sets into Borel sets.

A measure μ on the Borel subsets of G is called left-translation-invariant if and only if for all Borel subsets S of G and all a in G one has

$\mu(a S) = \mu(S). \quad$

A similar definition is made for right translation invariance.

Haar's theorem

There is, up to a positive multiplicative constant, a unique countably additive, nontrivial measure μ on the Borel subsets of G satisfying the following properties:

μ(gE) = μ(E) for any g in G and Borel set E (left-translation-invariance).

μ(K) is finite for every compact set K.

Every Borel set E is outer regular:

$\mu(E) = \inf \{\mu(U): E \subseteq U, U \text{ open}\}.$

Every open set E is inner regular:

$\mu(E) = \sup \{\mu(K): K \subseteq E, K \text{ compact}\}.$

Such a measure on G is called a left Haar measure. It can be shown as a consequence of the above properties that μ(U) > 0 for every non-empty open subset U. In particular, if G is compact then μ(G) is finite and positive, so we can uniquely specify a left Haar measure on G by adding the normalization condition μ(G) = 1.

The left Haar measure satisfies the inner regularity condition for all σ-finite Borel sets, but may not be inner regular for all Borel sets. For example, the product of the unit circle (with its usual topology) and the real line with the discrete topology is a locally compact group with the product topology and Haar measure on this group is not inner regular for the closed subset {1} x [0,1]. (Compact subsets of this vertical segment are finite sets and points have measure 0, so the measure of any compact subset of this vertical segment is 0. But, using outer regularity, one can show the segment has infinite measure.)

The existence and uniqueness (up to scaling) of a left Haar measure was first proven in full generality by André Weil.^[3] Weil's proof used the axiom of choice and Henri Cartan furnished a proof which avoided its use.^[4] Cartan's proof also proves the existence and the uniqueness simultaneously. The special case of invariant measure for second countable locally compact groups had been shown by Haar in 1933.^[1]

The right Haar measure

It can also be proved that there exists a unique (up to multiplication by a positive constant) right-translation-invariant Borel measure ν satisfying the above regularity conditions and being finite on compact sets, but it need not coincide with the left-translation-invariant measure μ. The left and right Haar measures are the same only for so-called unimodular groups (see below). It is quite simple, though, to find a relationship between μ and ν.

Indeed, for a Borel set S, let us denote by 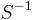$S^{-1}$ the set of inverses of elements of S. If we define

$\mu_{-1}(S) = \mu(S^{-1}) \quad$

then this is a right Haar measure. To show right invariance, apply the definition:

$\mu_{-1}(S a) = \mu((S a)^{-1}) = \mu(a^{-1} S^{-1}) = \mu(S^{-1}) = \mu_{-1}(S). \quad$

Because the right measure is unique, it follows that μ_-1 is a multiple of ν and so

$\mu(S^{-1})=k\nu(S)\,$

for all Borel sets S, where k is some positive constant.

Haar integral

Using the general theory of Lebesgue integration, one can then define an integral for all Borel measurable functions f on G. This integral is called the Haar integral. If μ is a left Haar measure, then

$\int_G f(sx) \ d\mu(x) = \int_G f(x) \ d\mu(x)$

for any integrable function f. This is immediate for step functions, being essentially the definition of left invariance.

Examples

A Haar measure on the topological group (R, +) which takes the value 1 on the interval [0,1] is equal to the restriction of Lebesgue measure to the Borel subsets of R. This can be generalized to (Rⁿ, +).

If G is the group of nonzero real numbers with multiplication as operation, then a Haar measure μ is given by

$\mu(S) = \int_S \frac{1}{|t|} \, dt$

for any Borel subset S of the nonzero reals.

This generalizes to the following:

For G = GL(n,R), any left Haar measure is a right Haar measure and one such measure μ is given by

$\mu(S) = \int_S {1\over |\det(X)|^n} \, dX$

where dX denotes the Lebesgue measure on R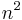, the set of all 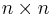$n\times n$ -matrices. This follows from the change of variables formula.

More generally, on any Lie group of dimension d a left Haar measure can be associated with any non-zero left-invariant d-form ω, as the Lebesgue measure |ω|; and similarly for right Haar measures. This means also that the modular function can be computed, as the absolute value of the determinant of the adjoint representation.

In order to define a Haar measure μ on the unit circle T, consider the function f from [0,2π] onto T defined by f(t) = (cos(t),sin(t)). Then μ can be defined by

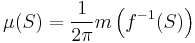$\mu(S)=\frac1{2\pi}m\left(f^{-1}(S)\right)$ ,

where m is the Lebesgue measure. The factor (2π)⁻¹ is chosen so that μ(T) = 1.

If G is the group of non-null quaternions, then G can be seen as an open subset of R⁴. A Haar measure μ is given by

$\mu(S)=\int_S\frac1{(x^2%2By^2%2Bz^2%2Bw^2)^2}\,dx\,dy\,dz\,dw$

where dx dy dz dw denotes the Lebesgue measure in R⁴ and S is a Borel subset of G.

Uses

Historically, the first use of the Haar theorem was the solution, by von Neumann, of Hilbert's fifth problem in the case of compact groups.^[5] In fact, von Neumann's article was published in the same issue of Annals of Mathematics as Haar's article and immediately after it.

The Haar measures are used in harmonic analysis on arbitrary locally compact groups; see Pontryagin duality. A frequently used technique for proving the existence of a Haar measure on a locally compact group G is showing the existence of a left invariant Radon measure on G.

In estimation theory, Haar measures can be used as non-informative priors, being Jeffreys priors for various questions. For instance, translation invariance of the (improper) uniform distribution on the real numbers (the Haar measure with respect to addition) corresponds to no information about location, and thus it is the Jeffreys prior for the unknown mean of a Gaussian distribution, the mean being a measure of location.

Unless G is a discrete group, it is impossible to define a countably-additive left invariant measure on all subsets of G, assuming the axiom of choice. See non-measurable sets.

The modular function

The left translate of a right Haar measure is a right Haar measure. More precisely, if μ is a right Haar measure, then

$A \mapsto \mu (t^{-1} A) \quad$

is also right invariant. Thus, by uniqueness of the Haar measure, there exists a function Δ from the group to the positive reals, called the Haar modulus, modular function or modular character, such that for every Borel set A

$\mu (t^{-1} A) = \Delta(t) \mu(A). \quad$

Since right Haar measure is well-defined up to a positive scaling factor, this equation shows the modular function is independent of the choice of right Haar measure in the above equation.

The modular function is a group homomorphism into the multiplicative group of nonzero real numbers. A group is unimodular if and only if the modular function is identically 1, or, equivalently, if the Haar measure is both left and right invartiant. Examples of unimodular groups are abelian groups, compact groups, discrete groups (e.g., finite groups), semisimple Lie groups and connected nilpotent Lie groups. An example of a non-unimodular group is the ax + b group of transformations of the form

$x \mapsto a x %2B b\quad$

on the real line. This example shows that a solvable Lie group need not be unimodular.

Notes

^ ^a ^b Haar, A. (1933), "Der Massbegriff in der Theorie der kontinuierlichen Gruppen", Annals of Mathematics, 2 34 (1): 147–169
^ We follow the conventions of Halmos' textbook. Nowadays, many authors instead use the term Borel algebra to denote the σ-algebra generated by the open sets.
^ Weil, André (1940), L'intégration dans les groupes topologiques et ses applications, Actualités Scientifiques et Industrielles, 869, Paris: Hermann
^ Cartan, Henri (1940), "Sur la mesure de Haar", Comptes Rendus de l'Académie des Sciences de Paris 211: 759–762
^ von Neumann, J. (1933), "Die Einfuhrung Analytischer Parameter in Topologischen Gruppen", Annals of Mathematics, 2 34 (1): 170–179

External links

On the Existence and Uniqueness of Invariant Measures on Locally Compact Groups - by Simon Rubinstein-Salzedo

Integrals

Methods	Riemann integral · Lebesgue integral · Burkill integral · Bochner integral · Daniell integral · Darboux integral · Henstock–Kurzweil integral · Haar integral · Hellinger integral · Kolmogorov integral · Lebesgue–Stieltjes integral · Pettis integral · Pfeffer integral · Riemann–Stieltjes integral · Regulated integral

Improper Integrals	Improper integral · Gaussian integral

Stochastic integrals	Itō integral · Stratonovich integral · Skorokhod integral